[ 복잡도 ] 시간 복잡도와 공간 복잡도

 

 

  컴퓨터 과학에서  "복잡도"란, 문제를 풀거나 알고리즘을 푸는데 필요한 리소스를 나타낸다. 이러한 복잡도는 문제를 푸는데 걸리는 시간을 나타내는 "시간 복잡도"와 문제를 해결하는데 필요한 메모리/스토리지 양을 나타내는 "공간 복잡도" 이 두가지를 포함하여 다양한 측면에서 평가될 수 있다.

 

1. 시간 복잡도

  시간 복잡도는 문제를 풀거나 알고리즘을 실행할 때 필요한 시간의 양을 나타내며, 일반적으로 입력 크기에 따라 측정된다. 이러한 시간 복잡도를 표기하기 위해 Big-O(상한 점근), Big-Ω(하한 점근), Big-θ(평균) 등의 표기법이 있는데, 주로 사용되는 것은 최악의 경우까지 고려할 수 있는 Big-O 표기법이다.

 

big O notation : 빅-오 표기법에서는 복잡도는 입력 (n)에 따라 평가되며, 일반적으로 문제를 해결하는 데 필요한 최대치의 작업 혹은 단계의 수로 표현된다.

 

1)  종류

 

1. O(1) : 상수 복잡도. 실행에 필요한 시간이 입력의 크기와 상관없이 항상 동일.
2. O(n) : 선형 복잡도. 실행에 필요한 시간이 입력의 크기에 정비례.
3. O(n^2) : 지수 복잡도. 실행에 필요한 시간이 입력의 크기의 제곱에 비례.
4. O(log n) : 로그 복잡도. 입력의 크기에 따라 실행에 필요한 시간이 log n 만큼 증가.
5. O(2^n) / O(n!) : 기하급수적 복잡도. 입력의 크기에 따라 실행에 필요한 시간이 기하급수적으로 증가

 

  

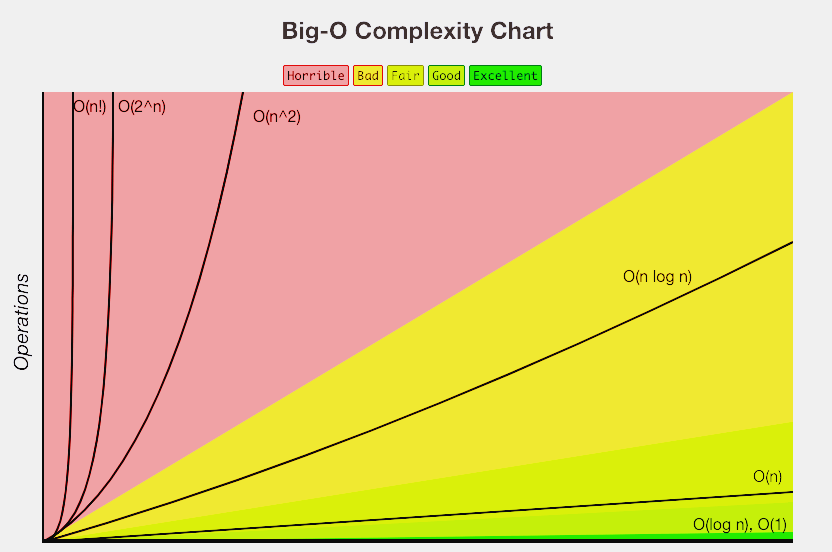
위 그래프에서 확인할 수 있듯이 입력 n의 계수가 복잡도에 미치는 영향을 미비하다.

 

 

2) O(1) 

  

operation	feature
arr[idx]	인덱스 연산자를 통한 배열 요소에 대한 접근
obj[idx], obj.idx	점 표기법 혹은 대괄호 표기법을 통한 객체 프로퍼티에 대한 접근
push()	배열 끝 요소 추가
pop()	배열 끝 요소 삭제

 

 

3) O(n) 

 

operation	feature	n
forEach(), reduce(), map(), filter()	배열을 통한 루핑	배열의 크기
indexOf(arg)	특정 원소의 인덱스를 찾기 위해 배열 전체를 탐색
includes(arg)	특정 원소의 포함 여부를 확인하기 위해 배열 전체를 탐색
unshift()	배열에 첫 번째 인덱스에 원소 추가
shift()	배열의 첫 번째 원소 제거

 

 

4) O(n^2)  

 

operation	example	featrue	n
for (condition) {     for (condition) {         .....     } }	bubbling sort insertion sort	중복 루프	바깥 루프의 사이즈

 

const arr = [1, 2, 3, 4, 5];

// O(n^2)
for (let i = 0; i < arr.length; i++) {
  for (let j = 0; j < arr.length; j++) {
    if (arr[i] < arr[j]) {
      [arr[i], arr[j]] = [arr[j], arr[i]];
    }
  }
}

 

5) O(log n) 

 

operation	feature	n
sort(fnc)	인자 fnc 따른 배열 원소 정렬	배열의 크기
binarySearch algorithm	이진 탐색 알고리즘
merge sort algorithm	병합 정렬

 

binarySearch 알고리즘 예시)

const arr = [1, 2, 3, 4, 5];

function binarySearch(arr, target) {
  let start = 0;
  let end = arr.length - 1;
  let mid;

  while (start <= end) {
    mid = Math.floor((start + end) / 2);

    if (arr[mid] === target) {
      return mid;
    } else if (arr[mid] < target) {
      start = mid + 1;
    } else {
      end = mid - 1;
    }
  }

  return -1;
}

binarySearch(arr, 3); // O(log n)

 

6) O(2^n) / O(n!) 

  자바스크립트의 내장 함수, 메서드 중 O(2^n) 혹은 O(n!)의 시간 복잡도를 가지는 것은 없으며 이러한 기하급수적 복잡도는 실제 문제를 해결하는데 실용적이지 않으므로 최대한 피하도록 하자

 

function fibo(n) {
  if (n <= 1) return 1;
  
  return fibo(n - 1) + fibo(n - 2);
}

 

 

2. 공간 복잡도

  공간 복잡도는 문제를 풀거나 알고리즘을 실행할 때 필요한 메모리/스토리지의 양을 나타내며, 시간 복잡도와 같이 입력 크기에 따라 측정된다. 당연히 더 낮은 공간복잡도를 요하는 알고리즘일수록 효율적이며, 이러한 공간 복잡도는 데이터를 저장하고 조작하기 위한 자료구조, 변수의 개수, 필요한 임시변수, 인풋의 크기 등에 영향을 받는다.

  간단하게 생각하면 스택에 호출되는 함수, 변수가 많아질수록 공간 복잡도 또한 증가한다고 생각할 수 있다. 공간 복잡도 또한 빅-오 표기법으로 나타낼 수 있으며 아래 예시를 통해 확인해보자.

 

1)  종류

 

1. O(1) : 상수 복잡도. 실행에 필요한 메모리의 크기가 입력의 크기와 독립적인 경우.
2. O(n) : 선형 복잡도. 실행에 필요한 메모리가 입력의 크기와 정비례한 경우
3. O(n^2) : 지수 복잡도. 실행에 필요한 메모리가 입력의 크기의 제곱에 비례.
4. O(log n) : 로그 복잡도. 입력의 크기에 따라 실행에 필요한 메모리가 log n 만큼 증가.

 

  공간 복잡도의 평가는 [ 전체 공간 요구 = 고정 공간 요구 + 가변 공간 요구] 로 이루어진다. 여기서 고정 공간 요구란 변수, 상수, 코드 저장 공간 등 입출력의 횟수나 크기와 상관없이 요구되는 공간이며, 가변 공간 요구는 특정 함수 호출, 인스턴스 생성, 함수의 순환 호출시 등 동적으로 필요한 공간 요구이다.

 

2) O(1) 

  아래 예시 코드의 경우 계산을 위해 x, y 두 변수만 사용하므로 요구되는 메모리는 입력의 크기에 영향을 받지 않는다.

 

function addTwoNumbers(x, y) {
  return x + y;
}

console.log(addTwoNumbers(1, 2)); // 3
console.log(addTwoNumbers(100, 200)); // 300

 

 

3) O(n) 

  아래 예시 코드의 경우 단일 루프를 통해 인자로 주어진 arr를 순회한다. 입력의 크기에 따라 총 반복횟수가 결정되며, 따라서 요구되는 메모리는 인자로 주어진 arr의 크기에 정비례한다. 

 

function sumArray(arr) {
  let sum = 0;
  for (let i = 0; i < arr.length; i++) {
    sum += arr[i];
  }
  return sum;
}

console.log(sumArray([1, 2, 3, 4, 5])); // 15
console.log(sumArray([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])); // 55
console.log(sumArray([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])); // 120

 

4) O(n^2)  

  아래 코드는 두 중첩 루프를 사용해 인자로 주어진 arr을 순회한다. 입력의 크기에 따라 반복 횟수가 결정되며 총 반복횟수는 입력의 크기의 제곱에 비례한다.

 

function printAllPairs(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      console.log(arr[i], arr[j]);
    }
  }
}

printAllPairs([1, 2, 3, 4, 5]);

 

5) O(log n)  

  아래 코드는 이진 탐색 알고리즘을 구현한 코드이다. 입력 인자의 크기가 순환의 횟수를 결정하고, 알고리즘에 따라 순환의 횟수가 대수적으로 증가한다. 

 

function binarySearch(arr, target) {
  let start = 0;
  let end = arr.length - 1;
  let mid;

  while (start <= end) {
    mid = Math.floor((start + end) / 2);

    if (arr[mid] === target) {
      return mid;
    } else if (arr[mid] < target) {
      start = mid + 1;
    } else {
      end = mid - 1;
    }
  }

  return -1;
}

binarySearch([1, 2, 3, 4, 5], 3);

 

6) O(2^n) / O(n!) 

  아래 예시코드에서는 재귀가 사용해 인자로 주어진 arr의 부분 배열을 모두 생성한다. 입력의 크기에 따라 재귀적 호출의 횟수가 결정되며 이러한 호출 수는 기하급수적으로 증가한다.

function generatePowerSet(arr) {
  if (arr.length === 0) {
    return [[]];
  }

  const subset = generatePowerSet(arr.slice(1));
  return subset.concat(subset.map(set => set.concat(arr[0])));
}

generatePowerSet([1, 2, 3]);