-
[ 비선형 자료구조 ] 우선순위 큐(Priority Queue) & 힙(Heap)Computer Science/자료 구조 2023. 1. 20. 15:46반응형
1. 우선순위 큐(priority queue)
1) 개념
FIFO 규칙을 따르는 일반적인 큐와는 다르게, 데이터간 우선순위를 할당하고 우선순위에 따른 보다 효율적인 삽입, 삭제등의 연산을 구현한 추상 자료구조를 우선순위 큐라한다. 따라서, 우선순위 큐에선 높은 우선순위를 지닌 요소가 비교적 낮은 요소보다 앞서 디큐, 접근된다.
2) 특징
우선순위 큐는 배열 운영 체제, 네트워크 라우팅 알고리즘, 데이터 압축 알고리즘 등에서 널리 사용되, 연결리스트 등을 이용해 구현 가능하지만 삽입, 삭제 연산의 시간복잡도 측면에서 힙을 사용하는 것이 효율적이기 때문에 일반적으로 힙을 사용해 구현한다. (배열이나 연결 리스트를 사용할 경우 우선순위가 중간쯤 위치한 데이터의 삽입 시 배열의 경우 대상 인덱스 이후의 모든 데이터의 인덱스를 조정해야하므로 O(n) 시간이 필요하고, 연결 리스트의 경우 해당 인덱스의 탐색에 시간이 많이 걸리므로 O(n) 시간이 필요하다. 이에 반해 힙의 경우 O(log n)의 시간복잡도를 갖는다.)
3) 종류
우선순위 큐의 주된 두 가지 타입은 max priority queue와 min priority queue이다. max priority queue의 경우 우선순위가 높은 데이터가 더 높은 가치를 갖으며, min priority queue의 경우 그 반대로 우선순위가 낮은 데이터가 높은 가치를 갖는다.
3) 구현
앞서 언급했듯이 우선순위 큐는 일반적으로 힙(heap)을 통해 구현되는 추상 자료구조이다. 힙은 그 종류에 따라 최대힙, 최소힙 등의 종류를 가진다. 힙에 저장할 자료형을 우선순위, 값 이 두가지의 프로퍼티를 가지는 객체로 정의하고 우선순위를 기준으로 힙을 정렬하며, 연산에 따라 객체를 저장하고 재정렬하거나, 객체를 힙 자료구조에서 지운 후 그 값을 반환하도록 한다면 손쉽게 우선순위큐의 구현이 가능하다.
2. 힙(heap)
1) 개념
힙은 완전 이진 트리 기반의 자료구조이다. 최대힙, 최소힙 두 종류로 구분되며 최대힙의 경우 루트노드에 가까울 수록 크고, 최소힙의 경우 루트 노드에 가까울 수록 작은값을 가진다. 힙에선 데이터의 중복이 허용되며, 주로 우선순위 큐를 구현하는데 사용된다. 나아가 힙 정렬, 데이크스트라의 최단경로 알고리즘 등에서도 사용된다.
2) 특징
- 완전 이진 트리 바탕의 자료구조이다.
- 우선 순위 큐 구현 및 힙 정렬 알고리즘에 사용된다.
- 중복된 값을 허용한다.
- 부모 자식간에 크기 차이만 비교한다.(형제 노드간에는 크기차이를 고려하지 않는다.)
3) 종류
(1) 최대힙
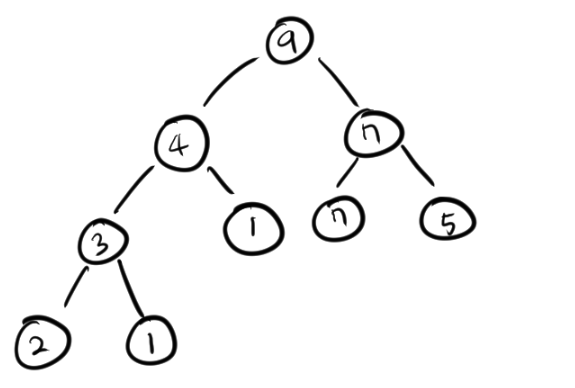
부모 노드의 키 값이 자식 노드 보다 크거나 같은 경우(루트 노드에 가까울수록 큰 값을 가진다.)
(2) 최소힙

부모 노드의 키 값이 자식 노드 보다 작거나 같은 경우 (루트 노드에 가까울수록 작은 값을 가진다.)
4) 구현
힙은 일반적으로 각 요소에 효율적으로 접근할 수 있는 배열을 통해 구현된다. 이때 0번째 인덱스의 사용 여부에 따라 약간의 차이를 가지는데, 아래 그림의 경우 0번째 인덱스를 사용하지 않는 경우를 나타낸다. 때문에, 인덱스 i에 위치한 노드의 부모는 i / 2 에 위치하며, 왼쪽 자식노드는 2i , 오른쪽 자식 노드는 2i + 1에 위치한다. (0번째 인덱스부터 데이터 값을 저장할 경우 부모는 (i - 1) / 2, 왼쪽 자식노드는 2i +1, 오른쪽 자식노드는 2i + 2의 인덱스를 갖는다.)

(1) 힙(heap)에서의 삽입
힙에서의 삭제는 새로운 요소를 힙의 가장 마지막 노드에 이어 추가한 뒤 해당 요소를 부모 요소와 비교해가며 힙의 특성에 맞추어 재배치한다. 순차적으로 나타내면 아래와 같다.
1.새로운 요소를 힙의 마지막 노드에 이어 추가한다.

2. 새로 삽입된 노드의 값을 부모 노드의 값 비교한다. 최소힙에서 새로 삽입된 노드가 부모 노드보다 작은 경우, 혹은, 최대힙에서 새롭 삽입된 노드가 부모 노드보다 큰 경우 두 요소를 교환한다. 이를 힙의 특성을 만족할 때까지 반복한다.

(2) 힙(heap)에서의 삭제
힙에서의 삭제는 root 노드를 지운 후 새로운 root를 자식 요소와 비교하고 재배치하며 힙의 특성을 만족하도록 재구성하는 것이다. 이를 순차적으로 나타내면 아래와 같다.
1. root노드를 삭제한다.
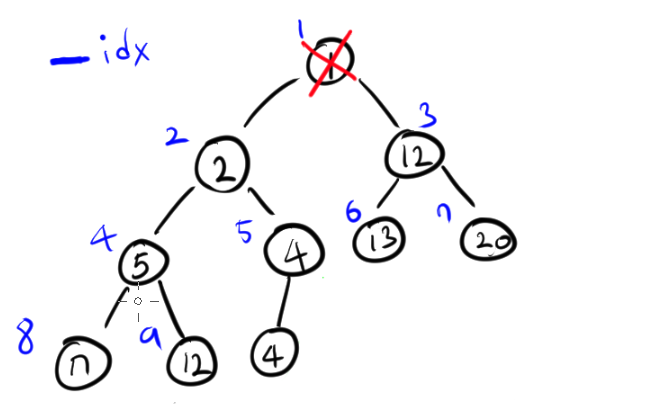
2. 삭제된 root 노드의 자리에 힙의 마지막 요소를 옮겨온다.

3. root노드와 자식 노드들을 비교하며 재배치한다. 최소힙의 경우 루트 노드가 자식 노드들보다 클 경우 더 작은 자식 노드와 자리를 바꾸고, 최대힙의 경우 루트노드가 자식 노드들 보다 작을 경우 큰 자식 노드와 자리를 바꾼다. 이를 힙의 특성이 만족될때까지 반복한다.

(3) JS 에서의 구현(min-heap)
class MinHeap { // idx = 1에 min value 저장 constructor() { this.heap = []; } isBiggerThanChildren(idx) { if (this.heap[2 * idx]) { return ( this.heap[idx] > this.heap[2 * idx] || this.heap[idx] > this.heap[2 * idx + 1] ); } else { return false; } } swapValue(idx1, idx2) { [this.heap[idx1], this.heap[idx2]] = [this.heap[idx2], this.heap[idx1]]; } insert(value) { this.heap.push(value); let currentIdx = this.heap.length - 1; let parentIdx = Math.floor(currentIdx / 2); while (currentIdx > 1 && this.heap[currentIdx] < this.heap[parentIdx]) { this.swapValue(currentIdx, parentIdx); currentIdx = parentIdx; parentIdx = Math.floor(currentIdx / 2); } } remove() { if (this.heap.length > 1) { if (this.heap.length === 2) return this.heap.pop(); let removedVal = this.heap[1]; this.heap[1] = this.heap.pop(); let currentIdx = 1; while (this.isBiggerThanChildren(currentIdx)) { if (this.heap[2 * currentIdx] < this.heap[currentIdx]) { this.swapValue(2 * currentIdx, currentIdx); currentIdx = 2 * currentIdx; } else if (this.heap[2 * currentIdx + 1] < this.heap[currentIdx]) { this.swapValue(2 * currentIdx + 1, currentIdx); currentIdx = 2 * currentIdx + 1; } } return removedVal; } else return null; } }반응형'Computer Science > 자료 구조' 카테고리의 다른 글
[ 비선형 자료구조 ] 맵(Map) & 셋(Set) (0) 2023.03.07 [ 비선형 자료구조 ] heapify & heap sort (0) 2023.03.05 [ 비선형 자료구조 ] 트리 순회 (0) 2023.01.19 [ 비선형 자료구조 ] 트리 (0) 2023.01.18 [ 비선형 자료구조] 그래프 (0) 2023.01.11