그래프의 탐색 - BFS, DFS

1. 너비 우선 탐색(BFS)

1) 개념

  너비 우선 탐색(BFS, Breadth-First Search)란 루트 노드 부터 시작해 인접한 노드를 우선적으로 탐색하는 방법이다. 이름 그대로 넓게 탐색하는 방법이며, 두 노드 사이의 최단 경로를 구하는 문제를 해결하는데 효과적이다.

 

  BFS의 구현과 이해는 Queue와 그래프에 대한 이해를 바탕으로 한다. 이에 대한 내용은 아래 글을 참고하면 된다.

 

[ 선형 자료구조 ] 스택(Stack) & 큐(Queue)

[ 비선형 자료구조] 그래프

 

2) 특징

• 최단 경로 탐색에 효과적이다.
• 노드 방문 여부를 검사해야 하므로 이에 대한 데이터가 필수적이다.
• 선입선출의 규칙을 따르는 자료구조인 큐를 사용한다.

 

3) 동작 방법

  BFS의 경우 노드의 방문 여부와 처리할 노드에 대한 데이터를 순서대로 저장해야 한다.방문 여부는 순서대로 저장되야 하므로 배열을 사용하고 처리할 데이터는 선입선출이 되어야 하므로 큐를 사용한다. 각 노드 방문 시(dequeue 연산 시) 인접 노드를 배열과 큐에 저장한다. 이러한 절차를 큐가 빌 때 까지 계속하면 되는데, 글로 설명하는 것 보다 그림을 통해 이해하는게 쉬우니 아래 그림을 참고하자.(초록색은 방문한 노드, 빨간색은 dequeue 연산 후 처리 중인 노드이다.)

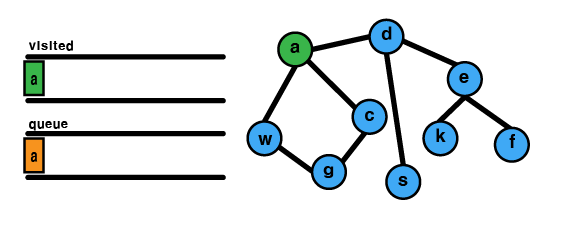
(1) 노드 a를 시작지점으로 설정. a방문 처리 및 enqueue 연산

(2) a dequeu 후 처리, w, c, d 방문 후 enqueue

(3) w dequeue 후 처리, g 방문 후 enqueue

(4) c dequeu, g의 경우 visited에 있으므로 패스

(5) d dequeue 후 처리, s, e 방문 및 enqueue

(6) g dequeue 후 처리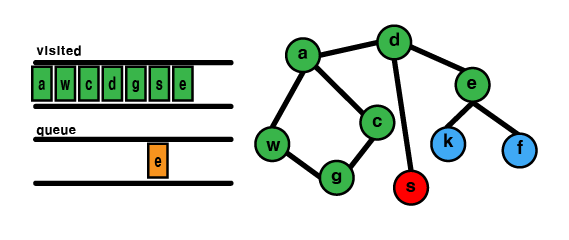

(7) s dequeue 후 처리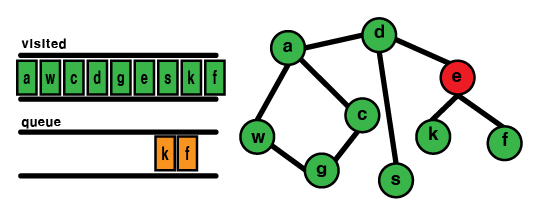

(8) e dequeue 후 처리, k, f 방문 후 enqueue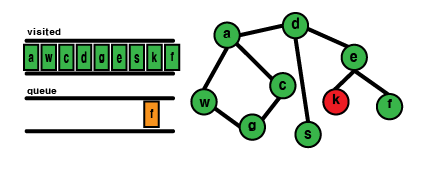

(9) k dequeue 후 처리

(10) f dequeue 후 처리, 더 이상 탐색할 노드가 없으므로(큐에 데이터가 없으므로) 종료

 

 

4) BFS 구현 - javascript

 

// 선형 큐
class Queue {
  constructor() {
    this.container = {};
    this.front = -1;
    this.rear = -1;
  }

  enQueue(item) {
    if (this.front === -1) {
      this.front++;
      this.rear++;
    } else {
      this.rear++;
    }

    this.container[this.rear] = item;
  }

  deQueue() {
    if (this.front === -1) return undefined;

    let temp = this.container[this.front];
    delete this.container[this.front];

    if (this.front === this.rear) {
      this.front = -1;
      this.rear = -1;
    } else {
      this.front += 1;
    }

    return temp;
  }

  peek() {
    return this.container[this.front];
  }

  isEmpty() {
    if (this.front === -1) return true;
    else return false;
  }

  print() {
    return this.container;
  }
}

// BFS 함수 구현
function BFS(graph, node) {
  let queue = new Queue();
  let visited = new Array();

  visited.push(node);
  queue.enQueue(node);

  while (!queue.isEmpty()) {
    let target = queue.deQueue();

    for (let n of graph[target]) {
      if (visited.includes(n)) continue;

      visited.push(n);
      queue.enQueue(n);
    }
  }

  return visited;
}

// 인접 리스트 방식의 그래프
let graph = {
  a: ["w", "c", "d"],
  w: ["a", "g"],
  c: ["a", "g"],
  d: ["a", "s", "e"],
  g: ["w", "c"],
  s: ["d"],
  e: ["d", "k", "f"],
  k: ["e"],
  f: ["e"],
};

 

 

2. 깊이 우선 탐색(DFS)

1) 개념

  루트 노드부터 다음 branch로 넘어가기 전에 해당 branch를 모두 방문하는 방법.

 

2) 특징

• BFS보다 간단하나 느리다.
• 순환 알고리즘의 형태를 취한다. 재귀 혹은 스택을 사용한다.
• 트리의 순회에 사용된다.
• 노드 방문 여부를 검사해야 하므로 방문 여부에 대한 데이터가 필수적이다.

3) 동작 방법

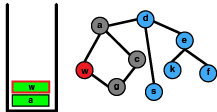
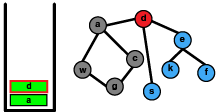
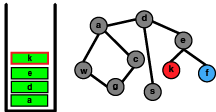
  DFS의 동작 방법은 루트 노드에서 부터 시작해 특정 branch에 진입한뒤 방문 기록이 없는 branch/인접노드들을 최대한 방문하는 것이다. 만약 더이상 방문 기록이 없는 인접 노드가 없는 상황에 다다랐을 경우 지나쳐온 노드들을 거슬러 올라가며 방문 기록이 없는지 검사하고 만약 방문 기록이 없는 인접 노드가 있을 경우 앞서 설명했던 동작을 반복한다.

 

  아래 그림에서 빨간색은 현재 방문한 노드로 stack의 top이며 회색은 방문 처리된 노드이다. 방향은 왼쪽에서 부터 오른쪽이다.   

1                                        2                                        3

4                                        5                                        6

7                                        8                                         9

10                                       11                                       12

13                                        14                                        15

16                                        17                                         18

 

 

4) DFS 구현 - Javascript

 

stack 사용 시)

function DFS(graph, node) {
  let visited = new Array();
  let stack = new Array();

  stack.push(node);

  while (stack.length) {
    let target = stack.at(-1);

    if (!visited.includes(target)) visited.push(target);

    let unvisited = graph[target].filter((ele) => !visited.includes(ele));

    if (unvisited.length === 0) stack.pop();
    else stack.push(unvisited[0]); 
  }

  return visited;
}

let graph = {
  a: ["w", "c", "d"],
  w: ["a", "g"],
  c: ["a", "g"],
  d: ["a", "s", "e"],
  g: ["w", "c"],
  s: ["d"],
  e: ["d", "k", "f"],
  k: ["e"],
  f: ["e"],
};

 

 

 

재귀 호출 사용 시)

function DFS(graph, node, visited = []) {
  if (visited.length === Object.keys(graph).length) return visited;
  if (visited.length === 0) visited.push(node);

  let adjacent = graph[node];
  let unvisited = adjacent.filter((ele) => !visited.includes(ele));

  if (unvisited.length === 0) {
    let idx = visited.indexOf(node);

    if (idx === -1) {
      visited.push(node);
      return DFS(graph, visited.at(-2), visited);
    } else {
      return DFS(graph, visited[idx - 1], visited);
    }
  } else {
    visited.push(unvisited[0]);
    return DFS(graph, unvisited[0], visited);
  }
}

let graph = {
  a: ["w", "c", "d"],
  w: ["a", "g"],
  c: ["a", "g"],
  d: ["a", "s", "e"],
  g: ["w", "c"],
  s: ["d"],
  e: ["d", "k", "f"],
  k: ["e"],
  f: ["e"],
};

console.log(DFS(graph, "a"));